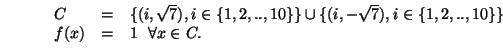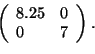suivant: Sélection du plan de
monter: Étude détaillée de l'approche
précédent: Sélection du multi-ensemble à
Table des matières
Index
Sélection de l'axe de découpe d'un multi-ensemble
Une fois que le multi-ensemble à découper a été
sélectionné, il faut choisir la normale du plan qui va couper
celui-ci. La décroissance de l'erreur de la partition induite par la
coupe étant égale à
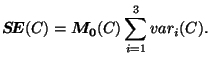 ,
le meilleur plan de découpe est celui qui minimise la somme
,
le meilleur plan de découpe est celui qui minimise la somme
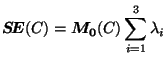 . Malheureusement, nous ne disposons pas
d'outils mathématiques permettant de calculer le plan optimal et une
énumération de tous les plans possibles est là encore
irréaliste. On simplifie donc le problème en déterminant d'abord
la normale au plan qui défini l'axe de coupe puis la position du
plan sur cet axe.
. Malheureusement, nous ne disposons pas
d'outils mathématiques permettant de calculer le plan optimal et une
énumération de tous les plans possibles est là encore
irréaliste. On simplifie donc le problème en déterminant d'abord
la normale au plan qui défini l'axe de coupe puis la position du
plan sur cet axe.
Un choix simple de l'axe de coupe a été proposé par
Heckbert [Hec82]. Celui-ci propose de découper l'axe de
coordonnée sur lequel le multi-ensemble à découper est le plus
étendu. Wu [WZ91] a étendu cette idée en choisissant
la direction de plus grande variance du multi-ensemble. Cette
direction est donnée par le vecteur propre associé à la plus
grande valeur propre de la matrice de covariance du multi-ensemble à
découper. Ce vecteur est plus simplement appelé l'axe
principal du multi-ensemble. La justification de cette heuristique
apparaît clairement lorsque l'on examine
l'équation 5.1 que nous rappelons ci-dessous :
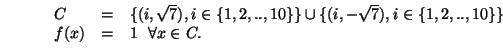 |
(6.8) |
Si l'on effectue un changement de repère en prenant pour nouvelle
base la base des vecteurs propres, l'équation 6.9 devient :
 |
(6.9) |
où  représente la
représente la  valeur propre et est
égale à la variance du multi-ensemble le long de la direction
définie par le
valeur propre et est
égale à la variance du multi-ensemble le long de la direction
définie par le 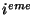 vecteur propre.
vecteur propre.
Si nous découpons le multi-ensemble perpendiculairement à un axe,
nous allons faire décroître majoritairement la variance suivant
cette axe. L'idée de base de l'heuristique de Wu consiste à
supposer que l'on obtient une plus grande décroissance de l'erreur
quadratique en faisant décroître en priorité la plus grande
des variances, c'est à dire en coupant perpendiculairement à l'axe
principal. Néanmoins, même si elle est très souvent vérifiée
pour des images réelles, cette heuristique peut être mise en
défaut. En effet, considérons l'exemple de la figure 6.6
où le multi-ensemble est défini par:
contrexLes points noirs sont les éléments de
dont l'axe principal est le vecteur
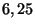 .
.
Dans cet exemple, la matrice de covariance de est alors
égale à :
Ceci signifie que l'axe principal de est le vecteur
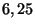 . Pourtant, si nous découpons perpendiculairement
au vecteur
. Pourtant, si nous découpons perpendiculairement
au vecteur 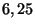 , l'erreur quadratique
, l'erreur quadratique 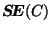 ne
décroîtra que de
ne
décroîtra que de 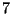 alors qu'un découpage perpendiculaire
à
alors qu'un découpage perpendiculaire
à 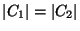 entraîne une diminution de
entraîne une diminution de 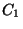 . Dans ce cas,
l'axe principal du multi-ensemble est donc orthogonal à la direction
de coupe optimale. C'est donc la direction la plus éloignée de
l'optimum.
. Dans ce cas,
l'axe principal du multi-ensemble est donc orthogonal à la direction
de coupe optimale. C'est donc la direction la plus éloignée de
l'optimum.
Outre qu'elle ne conduit pas nécessairement à la meilleure
solution, l'heuristique de Wu implique plusieurs contraintes
algorithmiques :
- Le fait de couper perpendiculairement à une direction
variable complique le traitement des données nécessaire au
découpage. Par exemple, avant d'effectuer un découpage,
l'algorithme de Wu doit trier les données de chaque multi-ensemble
suivant leur projection sur la direction de coupe.
- Le découpage d'un multi-ensemble réclame le calcul de la
matrice de covariance du multi-ensemble et le calcul de la plus grande
valeur propre de cette matrice. Le calcul du vecteur propre associé
s'effectue par une méthode itérative ce qui s'avère relativement
coûteux.





suivant: Sélection du plan de
monter: Étude détaillée de l'approche
précédent: Sélection du multi-ensemble à
Table des matières
Index
Brun Luc
2004-03-25
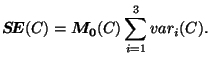 ,
le meilleur plan de découpe est celui qui minimise la somme
,
le meilleur plan de découpe est celui qui minimise la somme
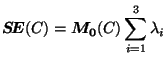 . Malheureusement, nous ne disposons pas
d'outils mathématiques permettant de calculer le plan optimal et une
énumération de tous les plans possibles est là encore
irréaliste. On simplifie donc le problème en déterminant d'abord
la normale au plan qui défini l'axe de coupe puis la position du
plan sur cet axe.
. Malheureusement, nous ne disposons pas
d'outils mathématiques permettant de calculer le plan optimal et une
énumération de tous les plans possibles est là encore
irréaliste. On simplifie donc le problème en déterminant d'abord
la normale au plan qui défini l'axe de coupe puis la position du
plan sur cet axe.