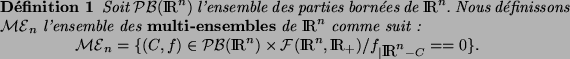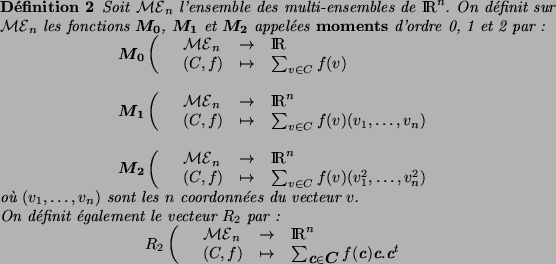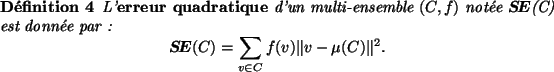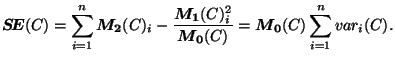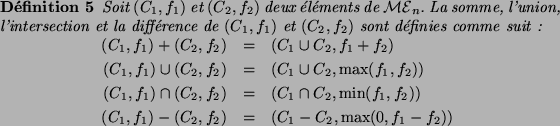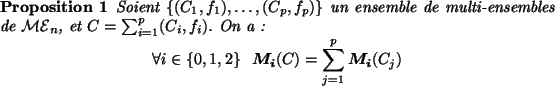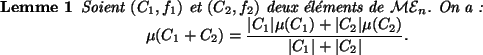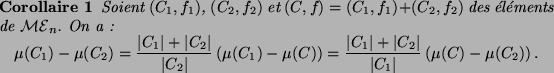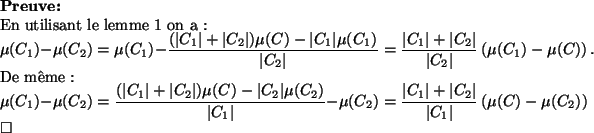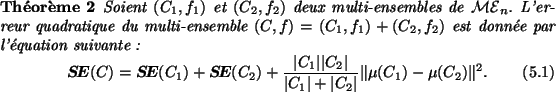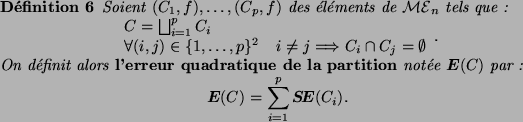suivant: Structures de données
monter: Histogramme d'images couleurs
précédent: Histogramme d'images couleurs
Table des matières
Index
Multi-ensembles
De façon très générale, un multi-ensemble est un élément
de
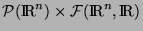 , où
, où
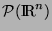 désigne l'ensemble des parties de
désigne l'ensemble des parties de 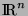 et
et
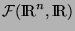 l'ensemble des applications de
l'ensemble des applications de 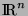 dans
dans 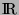 . Un multi-ensemble
est donc un couple
. Un multi-ensemble
est donc un couple 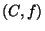 où
où 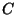 est un sous-ensemble de
est un sous-ensemble de 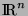 et
et
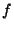 une application de
une application de 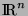 dans
dans 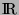 . Cette définition étant
un peu trop générale pour nos besoins, nous avons adopté la
définition suivante :
. Cette définition étant
un peu trop générale pour nos besoins, nous avons adopté la
définition suivante :
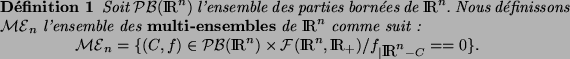
En d'autres termes, un multi-ensemble est la donnée d'un ensemble
borné et d'une application réelle positive nulle hors de cet
ensemble. Sauf mention contraire, tous les ensembles considérés
dans ce chapitre seront des ensembles discrets. D'un point de vue
informatique, les multi-ensembles peuvent être vus comme une
extension de la notion d'histogramme à des espaces de dimension 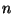 .
La fonction associée à un ensemble est souvent appelée la fonction de fréquence ou de distribution. L'application de ce concept à l'image est assez
immédiate. En effet, si nous considérons une image
.
La fonction associée à un ensemble est souvent appelée la fonction de fréquence ou de distribution. L'application de ce concept à l'image est assez
immédiate. En effet, si nous considérons une image 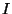 , on peut y
associer un ensemble
, on peut y
associer un ensemble 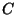 , égal à l'ensemble de valeurs
, égal à l'ensemble de valeurs 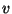 associées aux pixels de l'image. Nous pouvons alors définir
associées aux pixels de l'image. Nous pouvons alors définir 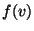 comme le nombre de fois où le n-uplet
comme le nombre de fois où le n-uplet
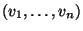 apparaît dans l'image. Par exemple, dans le cas d'une image
couleur,
apparaît dans l'image. Par exemple, dans le cas d'une image
couleur, 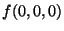 représente le nombre de pixels noirs contenus
dans l'image. La fonction de fréquence associe un poids à chaque
élément du multi-ensemble. Ces poids peuvent être utilisés
pour définir les moments, la moyenne ou la variance d'un
multi-ensemble.
représente le nombre de pixels noirs contenus
dans l'image. La fonction de fréquence associe un poids à chaque
élément du multi-ensemble. Ces poids peuvent être utilisés
pour définir les moments, la moyenne ou la variance d'un
multi-ensemble.
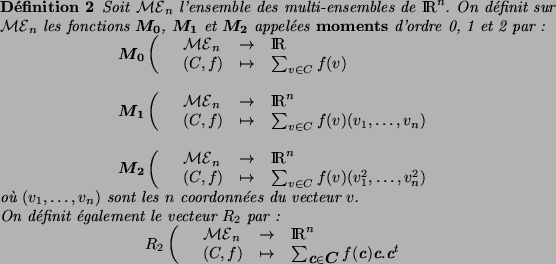
Il est bien sûr possible de définir des moments d'ordres supérieurs,
mais les ordres 0, 1 et 2 seront suffisants pour notre étude. Afin
d'alléger les notations, on omettra généralement la fonction de
fréquence lors du calcul de l'image d'un multi-ensemble. L'image de
par ,
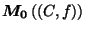 , sera donc notée plus
simplement
, sera donc notée plus
simplement 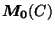 . On peut remarquer que (C) également noté
. On peut remarquer que (C) également noté
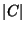 représente un scalaire alors que (C) et (C) sont des
vecteurs de
représente un scalaire alors que (C) et (C) sont des
vecteurs de 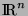 où
où 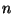 est la dimension de l'espace dans lequel est
plongé l'ensemble
est la dimension de l'espace dans lequel est
plongé l'ensemble 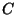 . Usuellement, cette dimension est égale à 1
pour les images en niveaux de gris et 3 pour les images couleur. À
partir des moments, on définit la moyenne, les variances et la matrice
de covariance d'un multi-ensemble de la façon suivante :
. Usuellement, cette dimension est égale à 1
pour les images en niveaux de gris et 3 pour les images couleur. À
partir des moments, on définit la moyenne, les variances et la matrice
de covariance d'un multi-ensemble de la façon suivante :

La fonction 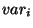 nous permet de mesurer la variance d'un
multi-ensemble le long d'un axe et peut servir à mesurer
l'homogénéité d'un multi-ensemble. La mesure d'homogénéité
que nous allons utiliser, appelée erreur quadratique, peut
être vue comme une extension de la variance pour les dimensions
supérieures à 1.
nous permet de mesurer la variance d'un
multi-ensemble le long d'un axe et peut servir à mesurer
l'homogénéité d'un multi-ensemble. La mesure d'homogénéité
que nous allons utiliser, appelée erreur quadratique, peut
être vue comme une extension de la variance pour les dimensions
supérieures à 1.
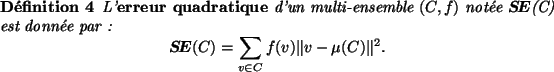
L'erreur quadratique d'un multi-ensemble 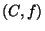 est donc une mesure
de l'écart des éléments de
est donc une mesure
de l'écart des éléments de 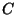 par rapport à la moyenne
par rapport à la moyenne
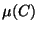 . Si nous appliquons ce concept à l'image, la moyenne
. Si nous appliquons ce concept à l'image, la moyenne
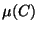 représente le niveau de gris moyen (ou la couleur moyenne)
de l'image et
représente le niveau de gris moyen (ou la couleur moyenne)
de l'image et 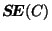 représente l'écart de l'ensemble des
couleurs de l'image par rapport à cette moyenne.
représente l'écart de l'ensemble des
couleurs de l'image par rapport à cette moyenne.
Des calculs relativement simples montrent que l'erreur quadratique
peut s'exprimer en fonction des moments et des variances. De fait, nous
avons pour un multi-ensemble 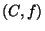 donné :
donné :
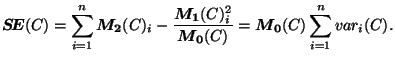 |
(5.1) |
L'erreur quadratique d'un multi-ensemble 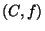 peut donc également
être vue comme la somme de ses variances pondérées par le
cardinal de
peut donc également
être vue comme la somme de ses variances pondérées par le
cardinal de 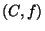 . Cette pondération permet de tenir compte du
fait qu'une même erreur est a priori plus importante si elle se
produit sur un grand ensemble que sur un petit.
. Cette pondération permet de tenir compte du
fait qu'une même erreur est a priori plus importante si elle se
produit sur un grand ensemble que sur un petit.
Jusqu'à présent, nous avons vu la définition d'un multi-ensemble
et les différentes mesures que l'on peut associer à celui-ci. Les
multi-ensembles peuvent également être combinés pour créer de
nouveaux multi-ensembles.
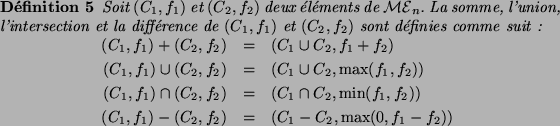
La combinaison de plusieurs multi-ensembles prend tout son intérêt
en segmentation lorsque l'on manipule une image partitionnée en
régions. Supposons par exemple que l'on désire fusionner deux
régions 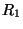 et
et 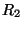 adjacentes dans l'image. Les multi-ensembles
adjacentes dans l'image. Les multi-ensembles
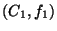 et
et 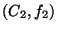 correspondant à
correspondant à 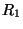 et
et 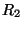 ne sont a
priori pas distincts. Le multi-ensemble correspondant à la fusion
des régions
ne sont a
priori pas distincts. Le multi-ensemble correspondant à la fusion
des régions 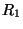 et
et 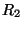 est alors égal à la somme des
multi-ensembles
est alors égal à la somme des
multi-ensembles 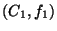 et
et 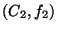 . Inversement, si on
désire partitionner une région
. Inversement, si on
désire partitionner une région 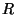 en deux sous-régions
en deux sous-régions 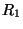 et
et
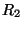 , nous avons la relation :
, nous avons la relation :
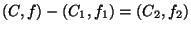 où
où
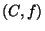 désigne le multi-ensemble associé à
désigne le multi-ensemble associé à  . Le problème
est alors d'évaluer l'erreur quadratique de l'union ou de la
différence de deux multi-ensembles. Un premier pas vers
l'évaluation de l'erreur quadratique est donné par la proposition
suivante:
. Le problème
est alors d'évaluer l'erreur quadratique de l'union ou de la
différence de deux multi-ensembles. Un premier pas vers
l'évaluation de l'erreur quadratique est donné par la proposition
suivante:
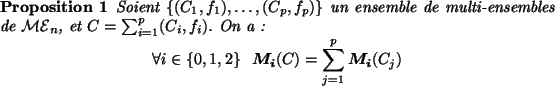

Une propriété importante de la moyenne se déduit trivialement de
l'additivité des moments :
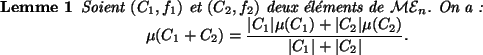
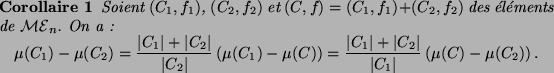
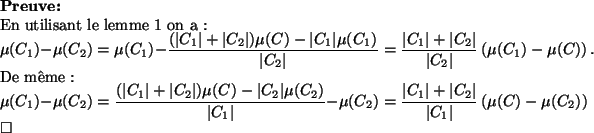
L'additivité des moments et le lemme précédent nous permettent de
définir un théorème important permettant d'exprimer l'erreur
quadratique de la somme de deux multi-ensembles.
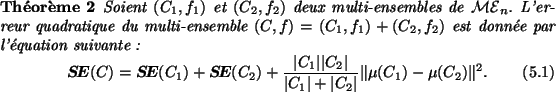

Comme nous l'avons vu, l'erreur quadratique 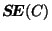 mesure
l'homogénéité de l'ensemble
mesure
l'homogénéité de l'ensemble 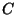 . Afin de mesurer
l'homogénéité d'une partition,
. Afin de mesurer
l'homogénéité d'une partition,
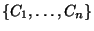 , on définit
l'erreur quadratique d'une partition de la façon suivante :
, on définit
l'erreur quadratique d'une partition de la façon suivante :
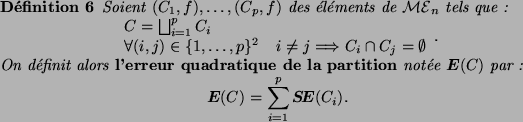
La partition de 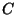 en sous-ensembles minimisant
en sous-ensembles minimisant 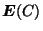 est un
problème complet pour des espaces de dimension supérieure
à 1 [WZ91]. Dans le cas mono-dimensionnel, donc pour des
images en niveaux de gris, Wong, Wan et Prusinkiewicz ont élaboré
un algorithme permettant de trouver la partition optimale avec une
complexité en
est un
problème complet pour des espaces de dimension supérieure
à 1 [WZ91]. Dans le cas mono-dimensionnel, donc pour des
images en niveaux de gris, Wong, Wan et Prusinkiewicz ont élaboré
un algorithme permettant de trouver la partition optimale avec une
complexité en 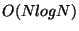 [WWP89].
[WWP89].
Le découpage d'un multi-ensemble s'effectue souvent en considérant
un de ses sous-ensembles et en faisant croître celui-ci jusqu'à
obtenir une partition qui induit une erreur quadratique minimale. Du
fait de la complexité du problème on ne choisit généralement
pas la partition qui minimise globalement l'erreur quadratique, mais
plus simplement la partition induisant une erreur quadratique minimale
sur un ensemble de partitions envisagées. La partition la plus
couramment utilisée est la partition par plans. Le
multi-ensemble est alors découpé en deux sous-ensembles de par et
d'autre du plan. Le nombre de plans susceptibles de couper un
multi-ensemble étant encore trop grand, on restreint les
possibilités en fixant la normale à celui-ci. L'ensemble des
partitionnements possibles est alors égal au nombre de plans
parallèles susceptibles de couper le multi-ensemble. Ce type de
découpe utilise la projection d'un multi-ensemble définie de
la façon suivante :

où 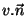 désigne le produit scalaire des vecteurs
désigne le produit scalaire des vecteurs 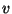 et
et
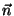 . La variable
. La variable 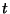 joue dans ce cadre le rôle d'une
abscisse le long de la direction
joue dans ce cadre le rôle d'une
abscisse le long de la direction 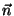 .
.





suivant: Structures de données
monter: Histogramme d'images couleurs
précédent: Histogramme d'images couleurs
Table des matières
Index
Brun Luc
2004-03-25