




suivant: Inversion de table de
monter: Étude détaillée de l'approche
précédent: Sélection de l'axe de
Table des matières
Index
Sélection du plan de coupe
Une fois sélectionnés le multi-ensemble à découper et
l'axe de coupe 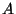 , nous devons définir la position du plan de coupe
le long de l'axe
, nous devons définir la position du plan de coupe
le long de l'axe 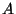 . La stratégie la plus simple est encore une
fois proposée par Heckbert [Hec82]. Celui-ci propose de
couper par un plan médian, c'est à dire un plan tel
que
. La stratégie la plus simple est encore une
fois proposée par Heckbert [Hec82]. Celui-ci propose de
couper par un plan médian, c'est à dire un plan tel
que
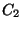 où
où 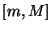 et
et 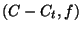 sont les deux multi-ensembles
issus de la découpe de .
sont les deux multi-ensembles
issus de la découpe de .
Cette stratégie peut être grandement améliorée en tenant
compte de l'erreur de la partition. En effet, soient 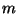 et
et 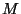 les deux
extrémités de le long de l'axe
les deux
extrémités de le long de l'axe 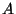 (voir
Figure 6.7 et définition 7) et
(voir
Figure 6.7 et définition 7) et 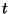 un
réel de l'intervalle
un
réel de l'intervalle ![$ [m,M]$](img954.png) . Le plan orthogonal
à
. Le plan orthogonal
à 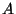 et de position
et de position 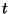 sur l'axe
sur l'axe 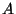 découpe en deux
multi-ensembles t et
découpe en deux
multi-ensembles t et 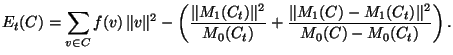 . L'erreur associée à
cette partition est égale à :
. L'erreur associée à
cette partition est égale à :
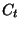 |
(6.10) |
clustersLe multi-ensemble sélectionné est découpé orthogonalement à l'axe de coupe 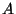 positionné à la coordonnée
positionné à la coordonnée 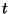 sur l'axe
sur l'axe 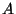 .
.
Wu [Wu92] a donné une autre formulation de l'erreur de la
partition :
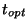 |
(6.11) |
Cette nouvelle formulation est plus efficace puisqu'elle ne fait
apparaître que le multi-ensemble 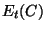 que nous allons faire
évoluer jusqu'à trouver la valeur
que nous allons faire
évoluer jusqu'à trouver la valeur 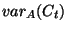 minimisant
minimisant
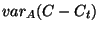 . Elle présente toutefois quelques
inconvénients. Tout d'abord elle impose de manipuler des grands
nombres tels que les moments d'ordre un au carré. Du point de vue
pratique, la présence de grands nombres oblige à stocker les
variables sur des entiers ou réels longs qui ralentissent
l'algorithme. De plus, cette formule se prête peu à des
manipulations et peut donc difficilement être optimisée.
. Elle présente toutefois quelques
inconvénients. Tout d'abord elle impose de manipuler des grands
nombres tels que les moments d'ordre un au carré. Du point de vue
pratique, la présence de grands nombres oblige à stocker les
variables sur des entiers ou réels longs qui ralentissent
l'algorithme. De plus, cette formule se prête peu à des
manipulations et peut donc difficilement être optimisée.
Wan et al. ont simplifié l'équation 6.12 en minimisant
non pas l'erreur de la partition mais la somme des variances
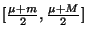 et
et
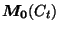 . Intuitivement, cette simplification
revient à approximer le multi-ensemble par sa projection
sur l'axe
. Intuitivement, cette simplification
revient à approximer le multi-ensemble par sa projection
sur l'axe 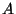 (voir définition 7). Afin de limiter la
perte d'information liée à cette simplification, Wan et
al. définissent
(voir définition 7). Afin de limiter la
perte d'information liée à cette simplification, Wan et
al. définissent 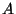 comme l'axe principal de . On peut
montrer que la recherche de la valeur
comme l'axe principal de . On peut
montrer que la recherche de la valeur 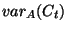 peut à ce moment là ce
limiter à l'intervalle
peut à ce moment là ce
limiter à l'intervalle
![$ [\frac{\mu+m}{2},\frac{\mu+M}{2}]$](img963.png) . Cette
approche permet donc de limiter l'intervalle de recherche mais ne
permet pas d'obtenir la position du plan minimisant l'erreur de la
partition.
. Cette
approche permet donc de limiter l'intervalle de recherche mais ne
permet pas d'obtenir la position du plan minimisant l'erreur de la
partition.
Le calcul de la valeur 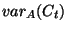 par les méthodes de Wu ou de Wan et
al. nécessite le calcul des moments
par les méthodes de Wu ou de Wan et
al. nécessite le calcul des moments 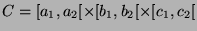 et
et 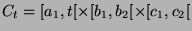 pour
pour
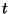 appartenant à l'intervalle
appartenant à l'intervalle ![$ [m,M]$](img954.png) . Ces moments peuvent être
calculés rapidement grâce à la propriété suivante. Supposons
que le multi-ensemble défini par
. Ces moments peuvent être
calculés rapidement grâce à la propriété suivante. Supposons
que le multi-ensemble défini par
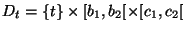 doit être découpé
perpendiculairement au premier axe de coordonnée. Pour tout
doit être découpé
perpendiculairement au premier axe de coordonnée. Pour tout 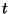 nous
avons alors :
nous
avons alors :
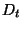 .
Si nous définissons :
.
Si nous définissons :
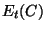 peut se définir comme l'union des
peut se définir comme l'union des 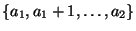 . Le multi-ensemble
étant discret, l'intervalle
. Le multi-ensemble
étant discret, l'intervalle ![$ [a_1,a_2]$](img970.png) est égal à
est égal à
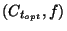 et les moments peuvent être calculés
incrémentalement par les formules suivantes :
et les moments peuvent être calculés
incrémentalement par les formules suivantes :
![$\displaystyle \forall i \in \{0,1,2\} \left \{ \begin{array}{l} M_{i}(C_{a+1})=...
...all t \in ]a+1,b[, M_{i}(C_{t+1})=M_{i}(C_t)+M_{i}(D_t). \\ \end{array} \right.$](img972.png) |
(6.12) |
Les moments du multi-ensemble
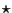 peuvent donc être
calculés incrémentalement à l'aide des
équations 6.13. Les moments du multi-ensemble
peuvent donc être
calculés incrémentalement à l'aide des
équations 6.13. Les moments du multi-ensemble
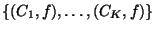 se déduisent des moments de
se déduisent des moments de
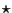 par la proposition 1 sur l'additivité des moments. Une
fois les moments des deux multi-ensembles calculés, on peut calculer
leurs moyennes, leurs variances et leurs erreurs quadratiques grâce
à la définitions 3 et à l'équation 5.1.
Les moments, moyennes et erreurs quadratiques de chacun des
multi-ensemble sont ensuite stockés dans les feuilles de l'arbre de
découpe correspondant aux multi-ensembles.
par la proposition 1 sur l'additivité des moments. Une
fois les moments des deux multi-ensembles calculés, on peut calculer
leurs moyennes, leurs variances et leurs erreurs quadratiques grâce
à la définitions 3 et à l'équation 5.1.
Les moments, moyennes et erreurs quadratiques de chacun des
multi-ensemble sont ensuite stockés dans les feuilles de l'arbre de
découpe correspondant aux multi-ensembles.





suivant: Inversion de table de
monter: Étude détaillée de l'approche
précédent: Sélection de l'axe de
Table des matières
Index
Brun Luc
2004-03-25
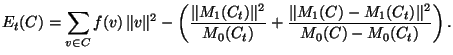 . L'erreur associée à
cette partition est égale à :
. L'erreur associée à
cette partition est égale à :
![]() et
et ![]() les deux
extrémités de le long de l'axe
les deux
extrémités de le long de l'axe ![]() (voir
Figure 6.7 et définition 7) et
(voir
Figure 6.7 et définition 7) et ![]() un
réel de l'intervalle
un
réel de l'intervalle ![]() . Le plan orthogonal
à
. Le plan orthogonal
à ![]() et de position
et de position ![]() sur l'axe
sur l'axe ![]() découpe en deux
multi-ensembles t et
découpe en deux
multi-ensembles t et 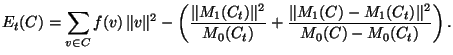 . L'erreur associée à
cette partition est égale à :
. L'erreur associée à
cette partition est égale à :
![]() positionné à la coordonnée
positionné à la coordonnée ![]() sur l'axe
sur l'axe ![]() .
.
![]() et
et
![]() . Intuitivement, cette simplification
revient à approximer le multi-ensemble par sa projection
sur l'axe
. Intuitivement, cette simplification
revient à approximer le multi-ensemble par sa projection
sur l'axe ![]() (voir définition 7). Afin de limiter la
perte d'information liée à cette simplification, Wan et
al. définissent
(voir définition 7). Afin de limiter la
perte d'information liée à cette simplification, Wan et
al. définissent ![]() comme l'axe principal de . On peut
montrer que la recherche de la valeur
comme l'axe principal de . On peut
montrer que la recherche de la valeur ![]() peut à ce moment là ce
limiter à l'intervalle
peut à ce moment là ce
limiter à l'intervalle
![]() . Cette
approche permet donc de limiter l'intervalle de recherche mais ne
permet pas d'obtenir la position du plan minimisant l'erreur de la
partition.
. Cette
approche permet donc de limiter l'intervalle de recherche mais ne
permet pas d'obtenir la position du plan minimisant l'erreur de la
partition.
![]() par les méthodes de Wu ou de Wan et
al. nécessite le calcul des moments
par les méthodes de Wu ou de Wan et
al. nécessite le calcul des moments ![]() et
et ![]() pour
pour
![]() appartenant à l'intervalle
appartenant à l'intervalle ![]() . Ces moments peuvent être
calculés rapidement grâce à la propriété suivante. Supposons
que le multi-ensemble défini par
. Ces moments peuvent être
calculés rapidement grâce à la propriété suivante. Supposons
que le multi-ensemble défini par
![]() doit être découpé
perpendiculairement au premier axe de coordonnée. Pour tout
doit être découpé
perpendiculairement au premier axe de coordonnée. Pour tout ![]() nous
avons alors :
nous
avons alors :
![]() .
Si nous définissons :
.
Si nous définissons :
![$ [a_1,a_2]$](img970.png) est égal à
est égal à