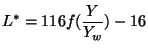 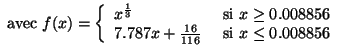 |
(4.6) |
Des expériences psycho-visuelles ont montré que l'appréciation des distances entre des stimuli mono-chromatiques pouvait être approximées par une racine cubique. La luminosité dans les deux espaces de couleurs et et donc définie par :
L_YLa luminosité ![]() en fonction de
en fonction de
![]()
La courbe représentée sur la Figure 4.7 présente plusieurs propriétés intéressantes : tout d'abord, l'on peut observer une pente importante aux faibles luminances. Cette propriété permet de tenir compte de l'intervention des bâtonnets (voir section 3.2) pour cet ordre de luminance. On observe également un effet de saturation pour les fortes luminances. De fait, de trop grandes luminances saturent les recepteurs de l'oeil et atténuent les différences de luminosité.
Les composantes chromatiques de l'espaces sont définies par :
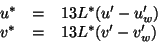
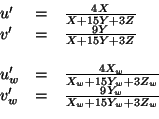
La coordonnée ![]() du modèle est définie de la même
façon que dans le modèle . Les coordonées chromatiques sont
définies par :
du modèle est définie de la même
façon que dans le modèle . Les coordonées chromatiques sont
définies par :
où la fonction ![]() est définie par l'équation 4.6.
est définie par l'équation 4.6.
Les coordonnées ![]() et
et ![]() représentent respectivement une
opposition entre les axes
représentent respectivement une
opposition entre les axes ![]() et
et ![]() et
et ![]() et
et ![]() . Les sensibilités
à chacun de ses axes sont à nouveau modélisées par la fonction
. Les sensibilités
à chacun de ses axes sont à nouveau modélisées par la fonction ![]() .
.
La distance entre deux couleurs ![]() et
et ![]() de coordonnées
de coordonnées
![]() et
et
![]() dans le système
et de coordonnées
dans le système
et de coordonnées
![]() et
et
![]() dans le système
est alors définie par la distance euclidienne :
dans le système
est alors définie par la distance euclidienne :
Suivant une étude menée sur le sujet par Pointer [Poi81], il semble qu'aucun des deux espaces CIE et ne soit significativement plus uniforme que l'autre. Il semble toutefois que l'espace tombe peu à peu en désuétude au bénéfice de l'espace .
La conversion entre les espaces et ou impose de passer par l'espace , de calculer une racine cubique et d'effectuer plusieurs divisions. Cette transformation implique donc souvent un surcoût de calcul non négligeable qu'il est souvent important de considérer lorsque l'on envisage le choix d'un espace de couleurs.