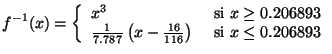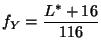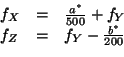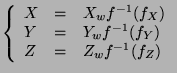suivant: Les espaces de couleurs
monter: Les espaces uniformes
précédent: Les espaces CIE et
Table des matières
Index
L'espace étant souvent utilisé on a souvent besoin de convertir
un triplet 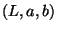 en un triplet affichable tel que (R,G,B). Cette
transformation nécessite de passer par l'espace puis d'utiliser
l'inverse de la matrice de conversion de vers .
en un triplet affichable tel que (R,G,B). Cette
transformation nécessite de passer par l'espace puis d'utiliser
l'inverse de la matrice de conversion de vers .
L'inverse de la fonction 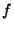 (équation 4.6) se
calcule aisément est est égal à :
(équation 4.6) se
calcule aisément est est égal à :
Si nous simplifions les notations en notant
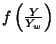 ,
,
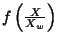 et
et
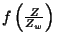 respectivement
respectivement 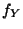 ,
, 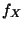 et
et 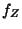 , il
vient immédiatement à partir de l'équation 4.6 :
De même, l'équation 4.7 constitue un système de deux équations
à deux inconnues dont les solutions sont :
On en déduit donc :
, il
vient immédiatement à partir de l'équation 4.6 :
De même, l'équation 4.7 constitue un système de deux équations
à deux inconnues dont les solutions sont :
On en déduit donc :
Brun Luc
2004-03-25
![]() en un triplet affichable tel que (R,G,B). Cette
transformation nécessite de passer par l'espace puis d'utiliser
l'inverse de la matrice de conversion de vers .
en un triplet affichable tel que (R,G,B). Cette
transformation nécessite de passer par l'espace puis d'utiliser
l'inverse de la matrice de conversion de vers .
![]() (équation 4.6) se
calcule aisément est est égal à :
(équation 4.6) se
calcule aisément est est égal à :