




suivant: Conclusion
monter: Opérateurs différentiels
précédent: Mise en oeuvre
Table des matières
Index
La couleur et les algorithmes de détection de contours
Nous avons vu dans la section 6.1 qu'une méthode
classique de segmentation d'image consiste à considérer une image
en niveau de gris comme la discrétisation d'une fonction 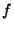 de
dans . À ce moment là les contours de l'image sont
définis comme les maxima de la différentielle première
de
dans . À ce moment là les contours de l'image sont
définis comme les maxima de la différentielle première 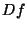 ou
les zéros de la différentielle seconde
ou
les zéros de la différentielle seconde 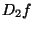 .
.
Si nous appliquons la même démarche à l'analyse d'images
couleurs, une image 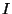 est considérée comme la discrétisation
d'une fonction
est considérée comme la discrétisation
d'une fonction 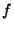 de dans . Nous avons alors :
de dans . Nous avons alors :
La différentielle première de 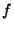 en
en 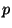 dans la direction
dans la direction 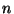 s'écrit alors :
Comme dans le cas mono-dimensionnel, nous recherchons les fortes
valeurs de la différentielle première. Cette différentielle
étant cette fois-ci un vecteur de , nous calculons le carré
de sa norme :
s'écrit alors :
Comme dans le cas mono-dimensionnel, nous recherchons les fortes
valeurs de la différentielle première. Cette différentielle
étant cette fois-ci un vecteur de , nous calculons le carré
de sa norme :
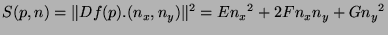 |
(6.4) |
avec :
L'équation 6.4 nous donne la norme de la
différentielle première dans la direction 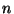 . Cette mesure nous
indique s'il existe ou non un contour au point
. Cette mesure nous
indique s'il existe ou non un contour au point 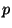 dans la direction
dans la direction
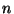 . L'existence d'un contour en
. L'existence d'un contour en 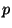 indépendamment de
indépendamment de 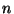 s'évalue
en cherchant le maximum de l'équation 6.4 pour
s'évalue
en cherchant le maximum de l'équation 6.4 pour 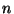 appartenant à la boule unité (seule la direction de
appartenant à la boule unité (seule la direction de 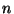 nous
intéresse). Si nous posons
nous
intéresse). Si nous posons
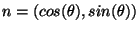 les
extrema de l'équation 6.4 sont atteints pour :
Le maximum correspondant est égal à :
La valeur
les
extrema de l'équation 6.4 sont atteints pour :
Le maximum correspondant est égal à :
La valeur 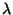 peut être vue comme l'extension du concept de
gradient aux images couleurs. En effet, on constate facilement que dans
le cas mono-dimensionnel,
peut être vue comme l'extension du concept de
gradient aux images couleurs. En effet, on constate facilement que dans
le cas mono-dimensionnel, 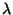 est égal au carré de la norme du
gradient. Il est donc naturel de considérer les passages par
zéro de la différentielle de la fonctions
est égal au carré de la norme du
gradient. Il est donc naturel de considérer les passages par
zéro de la différentielle de la fonctions 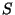 , au point
, au point 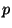 , dans
la direction
, dans
la direction 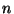 . Cette dernière valeur est donnée par
l'expression suivante :
où
. Cette dernière valeur est donnée par
l'expression suivante :
où 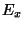 ,
, 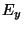 ,
,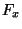 ,
, 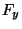 et
et 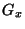 ,
, 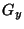 représentent les
dérivées partielles de
représentent les
dérivées partielles de 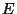 ,
, 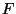 et
et 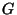 par rapport à
par rapport à 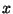 et
et 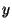 .
.
La valeur 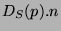 représente l'extension de l'opérateur
laplacien aux images multi-dimensionnelles.
représente l'extension de l'opérateur
laplacien aux images multi-dimensionnelles.
L'ensemble des techniques que nous venons de présenter semblent
avoir été découvertes en parallèle par Zenzo [Zen86]
et Cumani [Cum89,Cum91,CGG91]. Zenzo approxime
l'image en chaque pixel par trois fonctions linéaires (une pour
chaque composante). Ces approximations lui permettent de calculer les
dérivées partielles et d'en déduire la valeur de 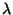 et
l'angle pour lequel le maximum est
réalisé. Chapron [Cha92] utilise les filtres de
Deriche [Der87] pour calculer les dérivées partielles
de l'image. Il combine ensuite ces dérivées pour obtenir la
fonction
et
l'angle pour lequel le maximum est
réalisé. Chapron [Cha92] utilise les filtres de
Deriche [Der87] pour calculer les dérivées partielles
de l'image. Il combine ensuite ces dérivées pour obtenir la
fonction 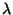 . Cumani [Cum89,Cum91,CGG91]
donne un ensemble d'outils théoriques permettant d'exploiter les
passages par zéros de la fonction
. Cumani [Cum89,Cum91,CGG91]
donne un ensemble d'outils théoriques permettant d'exploiter les
passages par zéros de la fonction 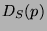 .
.





suivant: Conclusion
monter: Opérateurs différentiels
précédent: Mise en oeuvre
Table des matières
Index
Brun Luc
2004-03-25
![]() est considérée comme la discrétisation
d'une fonction
est considérée comme la discrétisation
d'une fonction ![]() de dans . Nous avons alors :
de dans . Nous avons alors :
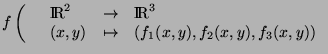
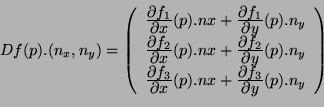
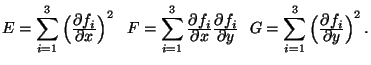
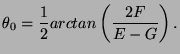
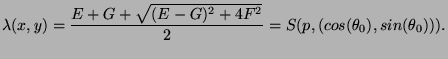
![]() représente l'extension de l'opérateur
laplacien aux images multi-dimensionnelles.
représente l'extension de l'opérateur
laplacien aux images multi-dimensionnelles.
![]() et
l'angle pour lequel le maximum est
réalisé. Chapron [Cha92] utilise les filtres de
Deriche [Der87] pour calculer les dérivées partielles
de l'image. Il combine ensuite ces dérivées pour obtenir la
fonction
et
l'angle pour lequel le maximum est
réalisé. Chapron [Cha92] utilise les filtres de
Deriche [Der87] pour calculer les dérivées partielles
de l'image. Il combine ensuite ces dérivées pour obtenir la
fonction ![]() . Cumani [Cum89,Cum91,CGG91]
donne un ensemble d'outils théoriques permettant d'exploiter les
passages par zéros de la fonction
. Cumani [Cum89,Cum91,CGG91]
donne un ensemble d'outils théoriques permettant d'exploiter les
passages par zéros de la fonction ![]() .
.