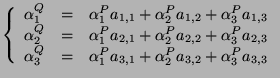suivant: Définition d'un espace couleur
monter: Correction des Exercices
précédent: Questions de compréhension
Table des matières
Index
Conversion entre espaces couleur
L'existence d'un triplet unique est justifiée par le fait que
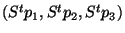 forme une base de
forme une base de 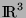 . Donc tout vecteur
s'écrit de manière unique dans cette base.
. Donc tout vecteur
s'écrit de manière unique dans cette base.
On déduit du cours que :
On obtient en exprimant
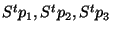 en fonction de
en fonction de
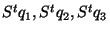 :
Or :
cette décomposition étant unique. On a donc :
:
Or :
cette décomposition étant unique. On a donc :
Autrement dit:
Brun Luc
2004-03-25