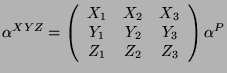
Cette matrice de conversion peut s'interpreter comme une matrice de
changement de base entre
![]() et
et
![]() , elle est donc inversible.
, elle est donc inversible.
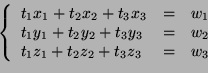
![$\displaystyle \left(
\begin{array}[c]{ccc}
x_1&x_2&x_3\\
y_1&y_2&y_3\\
z_1&z_...
...ray}\right)
=
\left(
\begin{array}[c]{c}
w_1\\ w_2\\ w_3\\
\end{array}\right)
$](img622.png)
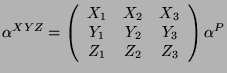
Cette matrice de conversion peut s'interpreter comme une matrice de
changement de base entre
![]() et
et
![]() , elle est donc inversible.
, elle est donc inversible.
![$\displaystyle \left(
\begin{array}[c]{ccc}
x_1&x_2&x_3\\
y_1&y_2&y_3\\
z_1&z_...
...ray}\right)
=
\left(
\begin{array}[c]{c}
w_1\\ w_2\\ w_3\\
\end{array}\right)
$](img622.png)