L'espace introduit par Otha et al. [OKS80] répond à une approche totalement différente. Otha, Kanade et Sakai ont cherché l'espace de couleurs présentant le plus d'intérêt pour la segmentation et le traitement d'images. Ils ont constaté que l'on obtenait de bons résultats en utilisant l'espace de couleurs défini par les trois axes de plus grande variance de l'ensemble des couleurs associé à l'image. Un résultat bien connu en analyse de données établit que ces axes correspondent aux vecteurs propres de la matrice de covariance de l'ensemble de couleurs associé à l'image (voir Figure 4.8).
cube_lennaMulti-ensemble associé à l'image Lenna. Les
vecteurs propres sont notés ![]() ,
, ![]() et
et ![]() dans l'ordre
décroissant de leurs valeurs propres. La longueur des vecteurs est
proportionnelle à leurs valeur propre.
dans l'ordre
décroissant de leurs valeurs propres. La longueur des vecteurs est
proportionnelle à leurs valeur propre.
Ce calcul des vecteurs propres de la matrice de covariance est souvent appelé la transformation de Karhunen-Loève dans la littérature anglo-saxone. Elle consiste à calculer tout d'abord la matrice de covariance définie par :
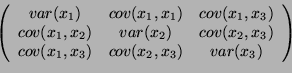
Cette matrice peut être calculée efficacement en utilisant les moments d'ordre 0, 1 et 2 de l'image :
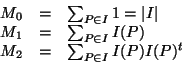
Notez que ![]() représente une valeur réelle alors que
représente une valeur réelle alors que ![]() est un
vecteur 3D et
est un
vecteur 3D et ![]() une matrice de taille
une matrice de taille ![]() . Etant donné les
moments
. Etant donné les
moments ![]() ,
, ![]() et
et ![]() (calculés en une passe de
l'image), la matrice de covariance est définie par [OB91] :
(calculés en une passe de
l'image), la matrice de covariance est définie par [OB91] :
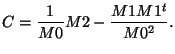
Cette matrice réelle et symétrique peut être diagonalisée sur
une base orthogonale égale aux vecteurs propres de
la matrice de covariance. De plus, chaque valeur propre de la matrice est égale à la variance de la projection des
couleurs de l'image sur le vecteur propre associé. L'information
portée par un vecteur propre ![]() est classiquement mesurée par :
est classiquement mesurée par :
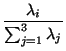
Les tests établis par Otha et confirmés par nos propres expériences (voir Table 4.1 ) montrent que les vecteurs propres d'une image ``naturelle'' s'écartent très peu de trois directions constantes. Le terme ``image naturelle'' s'oppose ici à ``image de synthèse''. On désignera par ``image naturelle'' une image habituellement perçue par l'oeil.
On constate sur la Table 4.1 que le vecteur propre de plus
grande valeur propre ![]() peut être approximé par le vecteur
peut être approximé par le vecteur
![]() . Ce vecteur définit un axe
vectoriel correspondant à la luminosité. Le second vecteur propre
. Ce vecteur définit un axe
vectoriel correspondant à la luminosité. Le second vecteur propre
![]() peut quant à lui être approximé par
peut quant à lui être approximé par
![]() . Ceci correspond à l'opposition
rouge-bleu. Le dernier vecteur propre
. Ceci correspond à l'opposition
rouge-bleu. Le dernier vecteur propre ![]() peut être approximé
par :
peut être approximé
par :
![]() ce qui correspond à
l'opposition vert-violet. Ces trois vecteurs fournissent une nouvelle
base permettant de définir un nouvel espace de couleurs déduit de
l'espace par la transformation suivante :
ce qui correspond à
l'opposition vert-violet. Ces trois vecteurs fournissent une nouvelle
base permettant de définir un nouvel espace de couleurs déduit de
l'espace par la transformation suivante :
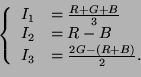
Le système contient donc un axe représentant la luminosité
et deux axes représentant la chromaticité. Remarquons que les axes
![]() et
et ![]() ont été multipliés par un facteur 2. Ceci
permet de renforcer l'importance de la chromaticité par rapport à
la luminosité afin d'être plus en adéquation avec la vision
humaine.
ont été multipliés par un facteur 2. Ceci
permet de renforcer l'importance de la chromaticité par rapport à
la luminosité afin d'être plus en adéquation avec la vision
humaine.