Beckmann modélise les micro-aspérités d'une surface à l'aide d'une
fonction aléatoire ![]() des variables
des variables ![]() et
et ![]() décrivant la
surface. La forme de la surface est donc déterminée par la densité de
probabilité de la fonction
décrivant la
surface. La forme de la surface est donc déterminée par la densité de
probabilité de la fonction ![]() . Beckmann propose d'utiliser une
distribution normale de moyenne nulle et d'écart type
. Beckmann propose d'utiliser une
distribution normale de moyenne nulle et d'écart type ![]() . La
distribution de
. La
distribution de ![]() est alors égale à :
est alors égale à :
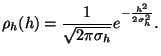
Toutefois, une telle modélisation ne permet pas un contrôle efficace de
la forme de la surface. En effet, plusieurs tirages aléatoires de la
fonction ![]() avec le même
avec le même ![]() peuvent présenter un aspect très
différent. Intuitivement, la raison de cette limitation est que le
paramètre
peuvent présenter un aspect très
différent. Intuitivement, la raison de cette limitation est que le
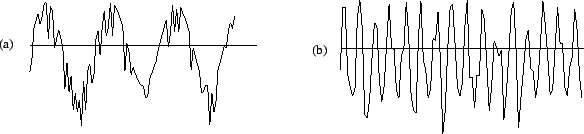
paramètre ![]() contrôle l'altitude moyenne des pics de la fonction
contrôle l'altitude moyenne des pics de la fonction
![]() mais pas l'écart entre deux pics (Figure 2.6).
mais pas l'écart entre deux pics (Figure 2.6).
 |
Afin de pallier à cette limitation, nous définissons un paramètre ![]() qui représente la corrélation entre les altitudes de deux points séparés
par une distance
qui représente la corrélation entre les altitudes de deux points séparés
par une distance ![]() . Beckmann propose de représenter cette
corrélation par la fonction :
. Beckmann propose de représenter cette
corrélation par la fonction :
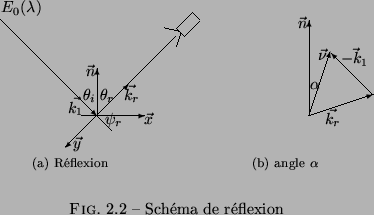
Étant donnée notre modélisation de la surface par les paramètres ![]() et
et ![]() , la position d'un patch de surface vis à vis de la source
lumineuse et de la caméra est représentée sur la
Figure 2.7(a). Le repère est choisi tel que
l'axe
, la position d'un patch de surface vis à vis de la source
lumineuse et de la caméra est représentée sur la
Figure 2.7(a). Le repère est choisi tel que
l'axe ![]() soit confondu avec la normale
soit confondu avec la normale ![]() et l'axe
et l'axe ![]() est
tel que le vecteur
est
tel que le vecteur
![]() décrivant la direction de la source
lumineuse soit dans le plan
décrivant la direction de la source
lumineuse soit dans le plan ![]() avec une projection positive sur
l'axe
avec une projection positive sur
l'axe ![]() . La puissance de la source lumineuse est décrite par la
norme de son vecteur de Poynting
. La puissance de la source lumineuse est décrite par la
norme de son vecteur de Poynting
![]() . Le vecteur
. Le vecteur ![]() décrit la direction de la caméra tandis que le vecteur
décrit la direction de la caméra tandis que le vecteur ![]() est
défini comme la bissectrice de
est
défini comme la bissectrice de
![]() et
et
![]() . Ce
vecteur fait un angle
. Ce
vecteur fait un angle ![]() avec la normale à la surface
(Figure 2.7(b)). Notez que le vecteur
avec la normale à la surface
(Figure 2.7(b)). Notez que le vecteur
![]() n'est pas nécessairement dans le même plan que
n'est pas nécessairement dans le même plan que ![]() et
et
![]() . L'angle
. L'angle ![]() représente son écart vis-à-vis de ce
plan (Figure 2.7(a)).
représente son écart vis-à-vis de ce
plan (Figure 2.7(a)).
Les paramètres
![]() et les variables illustrées sur la
Figure 2.7 étant définis,
Nayar [NIK91] en se basant sur les travaux de Beckmann, a
montré que l'irradiance à l'entrée d'un capteur
et les variables illustrées sur la
Figure 2.7 étant définis,
Nayar [NIK91] en se basant sur les travaux de Beckmann, a
montré que l'irradiance à l'entrée d'un capteur ![]() de la
caméra provoquée par un patch de surface d'un conducteur parfait de
cotés
de la
caméra provoquée par un patch de surface d'un conducteur parfait de
cotés ![]() et
et ![]() (Figure 2.8) pouvait être exprimée par :
(Figure 2.8) pouvait être exprimée par :
Les paramètres ![]() et
et ![]() dans l'équation 2.5 sont
relatifs à la caméra et illustrés sur la Figure 2.8. Notez
que pour une caméra placée raisonnablement loin de la scène nous
pouvons supposer
dans l'équation 2.5 sont
relatifs à la caméra et illustrés sur la Figure 2.8. Notez
que pour une caméra placée raisonnablement loin de la scène nous
pouvons supposer
![]() . Les termes
. Les termes ![]() ,
, ![]() ,
, ![]() et
et ![]() sont
issus de la résolution de l'intégrale d'Helmhotz et sont égaux à :
sont
issus de la résolution de l'intégrale d'Helmhotz et sont égaux à :
où
![]() (Figure 2.7(b)).
(Figure 2.7(b)).
reflexionRéflexion d' une onde électromagnétique frappant un des capteurs de la caméra
Le paramètre ![]() est proportionnel au carré du rapport
est proportionnel au carré du rapport
![]() qui représente le rapport entre l'altitude moyenne de nos irrégularités
et la longueur d'onde de la source incidente. Le facteur
qui représente le rapport entre l'altitude moyenne de nos irrégularités
et la longueur d'onde de la source incidente. Le facteur ![]() représente donc la rugosité de la surface et les cas
représente donc la rugosité de la surface et les cas ![]() ,
,
![]() et
et
![]() représenteront respectivement une surface lisse, modérément
rugueuse et rugueuse.
représenteront respectivement une surface lisse, modérément
rugueuse et rugueuse.
Le terme ![]() est une fonction qui décroît très rapidement dès que
est une fonction qui décroît très rapidement dès que
![]() ou
ou ![]() n'est pas proche de 0. Les coordonnées
n'est pas proche de 0. Les coordonnées ![]() et
et
![]() sont égales à 0 lorsque
sont égales à 0 lorsque
![]() est confondu avec
est confondu avec
![]() . Dans ce cas,
. Dans ce cas, ![]() est la bissectrice des vecteurs
sources et destination
est la bissectrice des vecteurs
sources et destination
![]() et
et
![]() . Ce type de
réflexion est appelé une réflexion spéculaire tandis que le terme
décrivant ce type de réflexion est appelé un pic
spéculaire. Le premier terme de
l'équation 2.5 correspond donc à une fonction pic dont
le maximum est atteint pour une réflexion spéculaire.
. Ce type de
réflexion est appelé une réflexion spéculaire tandis que le terme
décrivant ce type de réflexion est appelé un pic
spéculaire. Le premier terme de
l'équation 2.5 correspond donc à une fonction pic dont
le maximum est atteint pour une réflexion spéculaire.
Le second terme de l'équation 2.5 est appelé le
lobe spéculaire ; ce terme correspond à une
fonction qui prend son maximum lorsque la direction d'observation
correspond à la direction spéculaire mais décroît plus lentement que
le pic spéculaire. Notez tout de même le facteur
![]() qui décroît rapidement lorsque
qui décroît rapidement lorsque
![]() ne correspond pas à la direction spéculaire
(
ne correspond pas à la direction spéculaire
(
![]() ).
).
L'équation 2.5 se simplifie en fonction de la rugosité de la surface de la façon suivante :
Notez que pour ![]() , le lobe spéculaire est nul alors que le pic
spéculaire est maximum. Au fur et à mesure que la rugosité de la
surface augmente, le pic spéculaire diminue jusqu'à disparaître tandis
que le lobe spéculaire devient prépondérant.
, le lobe spéculaire est nul alors que le pic
spéculaire est maximum. Au fur et à mesure que la rugosité de la
surface augmente, le pic spéculaire diminue jusqu'à disparaître tandis
que le lobe spéculaire devient prépondérant.
Une description plus qualitative du pic et du lobe spéculaire sera donnée dans la Section 2.2.4; Nous pouvons toutefois dès à présent indiquer les conditions de validité de l'équation 2.5 :
Contrairement aux deux restrictions précédentes qui peuvent être ignorées dans la plupart des applications pratiques, cette dernière restriction interdit a priori d'utiliser l'équation 2.5 pour des isolants ou des matériaux de faible conductivité. Nous pouvons toutefois considérer que l'équation 2.5, sans nous donner une expression exacte de l'irradiance, nous fournit une bonne description qualitative du phénomène de réflexion à la surface d'un matériau. Cette hypothèse est confirmée par l'équation 2.9.