Le modèle Lambertien

Le modèle Lambertien est le modèle le plus utilisé pour décrire les phénomène de réflexion à l'intérieur des diélectriques. Ce modèle permet de relier l'irradiance incidente à un capteur à l'angle $\theta$ formé par l'onde incidente et la normale à la surface (Figure 2.2.1) à l'aide de l'équation suivante :

$$I=K_{diff}\cos(\theta)$$ (2.3)

où $K_{diff}$ est une constante dépendant du matériau.

Notez que dans un tel modèle la direction de l'observateur n'est pas prise en compte. Intuitivement, un objet Lambertien sera donc un objet dont la couleur ne varie pas lorsque l'on se déplace. Du bitume en milieu de journée fournit un bon exemple de surface Lambertienne.

Une explication qualitative de ce modèle généralement acceptée est la suivante : l'énergie incidente à une surface pénètre dans celle-ci et est réfléchie aléatoirement à l'intérieur de l'objet par de microscopiques in-homogénéités du matériau. Au cours de ces multiples réflexions une partie de l'énergie incidente est ré-émise par la surface et ressort de l'objet suivant une direction aléatoire. Les réflexions multiples dans le matériau ne subissant aucune contrainte particulière, l'énergie est ré-émise de façon uniforme par la surface. L'intensité de l'énergie émise par un point est donc indépendante de la direction d'observation et uniquement fonction de la quantité d'énergie incidente tombant sur la surface. Cette quantité s'exprime comme un cosinus de l'angle entre la normale à la surface et la direction de la source.

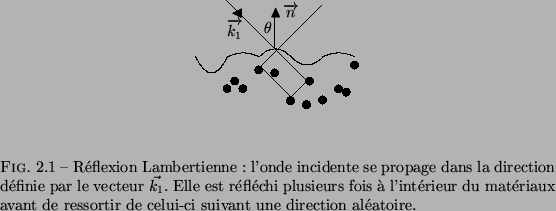
Une explication plus quantitative du modèle Lambertien peut être donnée dans le cas d'un diélectrique in-homogène. Ce type de matériau a été étudié par Reichmann [Rei73] qui à étendu un modèle initialement développé par Kubelka et Munk [KL31]. Reichmann modélise la répartition des pigments de colorants dans le matériau à l'aide d'un ensemble de couches superposées. L'interaction entre chaque couche élémentaire et l'onde incidente est décrite par les fonctions $\alpha(\lambda)$ et $\beta(\lambda)$ qui décrivent respectivement la fraction de l'onde incidente absorbée et réfléchie par unité de longueur.

La théorie de Kubelka et Munk repose sur la résolution de plusieurs équations différentielles du premier ordre dont la résolution fournit un coefficient de réflectance donné par :

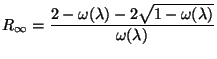$$R_{\infty}=\frac{2-\omega(\lambda)-2\sqrt{1-\omega(\lambda)}}{\omega(\lambda)}$$    avec $$\omega(\lambda)=\frac{\beta(\lambda)}{\alpha(\lambda)+\beta(\lambda)}$$

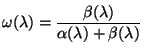
Toutefois, le modèle de Kubelka et Munk repose sur plusieurs hypothèses non réalistes dans le cadre d'applications réelles. Il suppose notamment que le matériau et l'air possèdent le même indice de réfraction afin d'éviter d'avoir à considérer les réflections à la surface du matériau. Ceci est visible dans la formule de $R_{\infty}$ qui ne dépend d'aucun paramètre géométrique.

L'extension proposée par Reichmann permet de lever ces limitations et nous donne une expression de la réflectance plus générale :

$$R_B(\theta,\lambda)=(1-R_S) \frac{C(\theta,\lambda)(1-r_i(\lambda... ...a)-D(\theta)\right)}{2\left(1-r_i(\lambda)R_\infty(\lambda)\right)\cos(\theta)}$$ (2.4)

où $R_S$ est la fraction de l'onde incidente réfléchie par la surface, ($1-R_S$) est donc la fraction de l'onde qui pénètre dans le matériau. Le terme $r_i(\lambda)$ représente la réflectance de surface interne du matériau [Orc69] tandis que les fonctions $C(\theta,\lambda)$ et $D(\theta)$ viennent de la résolution des équations du modèle et sont données par :

$$\begin{array}{lll} C(\theta,\lambda)&=& \frac{\omega(\lambda... ...theta)&=&\frac{2\cos(\theta)-1}{2\cos(\theta)+1}\\ \end{array}$$

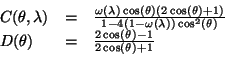
L'équation 2.4 semble beaucoup plus complexe que l'équation Lambertienne (équation 2.3). Toutefois dans le cas de matériaux n'absorbant pas l'onde incidente ( $\alpha(\lambda)\approx 0$) nous avons $\omega(\lambda)\approx 1$ et le lecteur peut vérifier que l'équation 2.4 se réécrit $R_B(\theta,\lambda)=(1-R_S)$. La partie de l'onde qui n'est pas réfléchie par la surface est donc renvoyée uniformément indépendamment de la longueur d'onde et de l'angle $\theta$ formé par l'onde incidente et la normale à la surface. On retrouve donc bien dans ce cas l'explication qualitative de la réflexion Lambertienne donnée au début de cette section. Notez toutefois que pour avoir une irradiance à l'entrée du capteur fonction uniquement de $\cos(\theta)$ nous devons supposer le terme $(1-R_S)$ approximativement constant. Cette hypothèse n'est pas valable dans le cas des matériaux conducteurs (voir par exemple la Section 2.2.2). Notons de plus que quelque soit le type du matériau celui ci acquiert un comportement spéculaire pour un angle d'incidence rasant ( $\theta\approx \frac{\pi}{2}$). Dans ce cas le modèle Lambertien n'est plus valable. Ce phénomène explique par exemple, les éblouissements dues à la réverbération du soleil sur le bitume au coucher du soleil.