Dans les cas usuels, la fonction ![]() comporte souvent du bruit. Ce
bruit peut parasiter la détection des contours de
comporte souvent du bruit. Ce
bruit peut parasiter la détection des contours de ![]() en créant
des sauts de valeurs artificiels. Un moyen simple de diminuer le bruit
est de convoluer la fonction
en créant
des sauts de valeurs artificiels. Un moyen simple de diminuer le bruit
est de convoluer la fonction ![]() avec un filtre passe-bas. La
convolution de deux fonctions
avec un filtre passe-bas. La
convolution de deux fonctions ![]() et
et ![]() de dans définit
la fonction
de dans définit
la fonction ![]() :
:
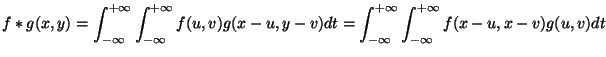
Une des principales raisons de la popularité de la gaussienne est sa
séparabilité. Si ![]() représente une gaussiennne 2D on
a :
représente une gaussiennne 2D on
a :
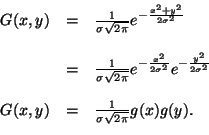
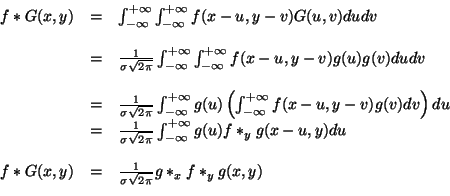
La convolution de ![]() avec la gaussienne 2D
avec la gaussienne 2D ![]() peut donc être
réalisée grâce à deux convolutions de signaux 1D. Ceci permet
d'utiliser deux convolutions avec des masques 1D
peut donc être
réalisée grâce à deux convolutions de signaux 1D. Ceci permet
d'utiliser deux convolutions avec des masques 1D
![]() plutôt qu'avec un masque 2D de taille
plutôt qu'avec un masque 2D de taille
![]() . Convoluer une image comportant
. Convoluer une image comportant ![]() pixels avec une gaussienne dont la taille du masque est égale à
pixels avec une gaussienne dont la taille du masque est égale à ![]() réclame donc 2mn opérations, l'utilisation d'un masque
2D réclamant quant à elle mn^2 opérations.
réclame donc 2mn opérations, l'utilisation d'un masque
2D réclamant quant à elle mn^2 opérations.
Une des propriétés essentielles du produit de convolution, en segmentation, est la possibilité de placer alternativement la dérivée sur un membre ou sur l'autre. Plus précisément on a :
Donc si ![]() représente l'image filtrée par une gaussienne, le
gradient de l'image filtrée peut tout simplement s'effectuer en
calculant la convolution de
représente l'image filtrée par une gaussienne, le
gradient de l'image filtrée peut tout simplement s'effectuer en
calculant la convolution de ![]() avec le gradient de G, G, qui
peut être précalculé une fois pour toute. De même, le filtrage
d'une image par une gaussienne
avec le gradient de G, G, qui
peut être précalculé une fois pour toute. De même, le filtrage
d'une image par une gaussienne ![]() , puis le calcul de son laplacien
peuvent s'effectuer grâce à une seule convolution
, puis le calcul de son laplacien
peuvent s'effectuer grâce à une seule convolution
![]() .
.