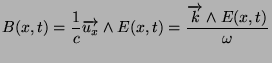suivant: Réflection d'une onde plane
monter: Les ondes électromagnétiques
précédent: Ondes planes
Table des matières
Index
Onde planes mono-chromatiques
Une onde plane sinusoidale monochromatique de longueur d'onde
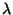 se déplaçant dans le vide à la vitesse
se déplaçant dans le vide à la vitesse 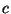 est définie par
l'équation :
si nous introduisons le vecteur d'onde
est définie par
l'équation :
si nous introduisons le vecteur d'onde
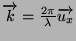 , nous obtenons :
avec
, nous obtenons :
avec
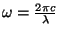 et
et
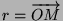 .
.
Le champ magnétique est alors donné par:
Les ondes électromagnétiques monochromatiques planes sont plus
aisément manipulables lorsque l'on travaille en notation complexe ; on
crée donc les champs complexes :
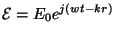
et
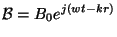
où 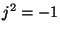 représente le nombre imaginaire pur.
représente le nombre imaginaire pur.
Dans ce cas, les champs électriques et magnétiques représentent la
partie réelle de ces expressions complexes. Les dérivées par rapport
au temps et à l'espace s'expriment alors aisément par :
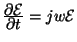
et
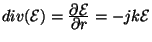
Les équations de Maxwell dans le vide se simplifient alors de la façon
suivante :
- Equation du flux conservatif :
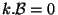
- Equation de Maxwell-Faraday :
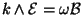
- Equation de Maxwell-Gauss:
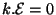
- Equation de Maxwell-Ampère:
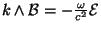
.





suivant: Réflection d'une onde plane
monter: Les ondes électromagnétiques
précédent: Ondes planes
Table des matières
Index
Brun Luc
2004-03-25